The Electron’s Anomalous Magnetic Moment

This Appendix is a slightly edited version of a chapter entitled ‘An Excursion in Quantum Electrodynamics’ which appears in my book: ‘Aether Science Papers’ published in 1996.

The starting point in the whole of my research has been the subject of electrodynamics and its energy anomalies, by which I mean the experimental anomalies and not the paradoxical notions that beset the theory of the subject.

I have found repeatedly, from my attempts to write about such matters, that referees of physics journals delight in pointing to the success of quantum electrodynamics in explaining the anomalous magnetic moment of the electron. They claim such precision in their calculations that is so overwhelming that surely only a fool would dare to think that, by contemplating an aether, there may be a better and easier way of going about that task.

So, having discovered the easy alternative, I delved into that wonderful world of QED to see how its magic derived a theoretical value for the g/2 factor of the electron which measurement shows as being 1.001159652193(10). This is the value adopted in consultation with the CODATA Task Group in 1986 and as made available to scientists in U.K. by a pocket chart published by The Royal Society jointly with other learned bodies. The numerical value just quoted is stated to be the magnetic moment of the electron in terms of the Bohr magneton.

I saw that a book entitled ‘Introduction to Gauge Field Theory’ had been authored by Bailin and Love and published in 1986 under the auspices of the Institute of Physics in U.K. and that the promotion literature specifically declared that it provided ‘a detailed treatment of quantum electrodynamics’. I bought that book with the express purpose of seeing exactly how those who really understand QED actually obtain the wonderfully precise number that one understands fits so well with the value measured.

In a browsing mood, I first opened the book on page 214 and was pleased to see that chapter 14 began with the words: “The spectacular success of quantum electrodynamics (QED) in calculating the Lamb shift and the anomalous magnetic moment of the electron and the muon …”. Yes, that statement meant that what I was looking for would be found in the earlier chapters of the book. After all, here was a book on that very subject.

I found the relevant section heading on page 140: ‘The electron anomalous magnetic moment’. The opening words were: “In this section, we specialise to the case of QED (Abelion gauge theory) and derive the electron anomalous magnetic moment. For convenience we shall work in the Feynman gauge…” I was expecting then to see the analysis develop to the derivation of something very close to that 1.001159652193(10) number recited above, but, to my horror, the derivation ended on page 142 with the words:

“Thus the anomalous magnetic moment of the electron µ_AMM is:

µ_AMM = (α/2π)(e/2m).”

Alpha, α, is a fundamental constant in atomic physics, the fine-structure constant. I knew that this was only the first-order determination, being the reciprocal of α/2π(137.036), which is 0.0011614. Evidently the ‘spectacular success’ was not something I could verify by guidance from that book. I was expected to accept that QED was a ‘spectacular success’ but it was something I had to take on trust without knowing what assumptions were made in the onward iterations of the calculation.

The book was, of course, full of equations, each one following the other and so conveying the impression of being ‘a tight logical structure’ but when the crunch came and a numerical result should have emerged I had to be satisfied with the above first-order approximation formula.

From my academic background in engineering I had always judged the result of a ‘tight logical structure’ on the end result, by comparing the numerical value derived with that observed as an actual experimental result.

I am now going to make the outrageous statement that QED is so powerful a technique that it is like taking a power-driven sledgehammer to crack a nut. There just has to be an easier way to explain how Nature determines that anomalous magnetic moment!

A back-of-an-envelope type of calculation can do better than that QED result presented in the book by Bailin and Love. All that is meant by the anomaly of the electron magnetic moment is that the antics of an electron in motion cannot bring to bear the electric energy in the far field zone fast enough to affect its inertia when in orbit having a very restricted radius. There is a cut-off range connected with the electron’s Compton wavelength and only the electric field energy within that range contributes to the electron’s inertia in its state of minor orbital motion.

This may be an engineer’s way of looking at the problem, but it is a realistic approach.

If what I have said above about the moving atom and its problems in collecting energy spread over its electromagnetic field is ‘phantasy’, then so the world of QED is phantasy of an extreme kind, because that goes even further by involving us in the problems of photon-electron interactions and something called ‘normalization’ to avoid infinities but which amounts to the ‘cut-off’ range just mentioned. So, I sit, in my aging years, watching the world of physics evolve its ‘tight logical structure’ and wonder if that world will ever look up my paper, ‘Fundamental Constants derived from Two-Dimensional Harmonic Oscillations in an Electrically-Structured Vacuum’, Speculations in Science and Technology, v. 9, 315-323 (1986). That paper shows, in a few pages, how the electron’s g/2-factor, can be explained with at least the same precision that is claimed for QED.

The formula is:

g/2 = 1 + α /[2π (1+3^1/2/Ν) − α] Here, N is determined as the nearest prime number to the value 3π/2α. Since α^-1 is just a little above 137, N is 647. The table below is reproduced from that referenced paper to show how g/2 depends upon the value of α^-1.

(alpha)-1	(g/2) factor
137.03597	1.001159652365
137.03598	1.001159652280
137.03599	1.001159652195

Now, that paper of mine was received by the publishing journal in November 1985 and at that time I, the author, was completely unaware of the prospect that the CODATA values to be adopted later in 1986 would establish 1.001159652193(10) as the g/2-factor of the electron. Nor did I imagine that the α^-1 value adopted would be 137.0359895(61).

What must then be absolutely clear to anyone reading this is the fact that if QED is a ‘spectacularly successful’ theory because it provides something very close to this relationship between the fine-structure constant and the anomalous magnetic moment of the electron, then it cannot be any closer than the value derived above using my very simple formula with N as 647.

What I offer, however, is a ‘back-of-the-envelope’ type of analysis for deducing that formula, whereas the eighth-order calculation based on numerous, indeed thousands of, Feynman diagrams as well as arbitrary hadronic involvements, as needed to get a close QED value, is a task that could well keep the reader fully occupied for several years. That assumes the reader has very advanced skills in the relevant mathematics, skills far in excess of the school-level training which suffices to understand my method.

As is well known, the electron exhibits a characteristic wave frequency, ν_c, which is the Compton electron frequency. This is the frequency of the photon corresponding to the mass-energy of an electron at rest. Now, although Einstein may have said that the idea that something can be at ‘rest’ is meaningless, I do not accept that. You see, it is a question of deciding whether each electron in the universe is a law unto itself so far as external governing influences are concerned, or whether it is regulated by external influence. I can assure you that that Compton electron frequency is a universal regulating rhythm that beats the time and all electrons have to dance to that time. They are not free to wander, each having its own proper time, much as Einstein might have wished that to be the case! If you have read in books about ‘time’ that there is no such thing as ‘universal time’ then you have exposed yourself to a ‘brainwashing’ exercise conducted by devil authors who preach the Einstein doctrine but contribute nothing to the science which sustains technological progress.

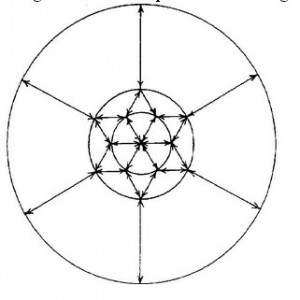
My method involves an energy cut-off range determined by a wave resonance in the near-field zone of the electron as shown in the figure below. The length of the radial lines in the outer cavity is half the Compton wavelength of the electron, because the field oscillations are phase-locked by the charge polarity condition. The length of the radial lines in the inner core of the electron charge is approximately the electron charge radius a and represents a standing wave condition of much higher frequency.

Now, the electron itself is a form of energy compressed into a field and we can calculate how that energy is distributed. J. J. Thomson did that calculation in the 19th century to find that, in electrostatic units, the energy e²/2α was seated outside the charge radius α. However, he discovered from the study of how electron mass increased with speed, even tending to become infinite as the speed of light was approached, that the effective rest mass of the electron was 2e²/3αc².

This meant that, if the electron were hollow within the radius a, then we could write the energy E as being 3Mc²/4. However, even before Einstein came into the picture in 1905, the Cambridge cosmologist, Sir James Jeans had, in his early years before being knighted, explained that mass and energy are equivalent and had argued that matter could be annihilated to produce radiant energy. He saw this as being the energy source feeding the sun and all other stars.

It is a simple exercise to work out that if the pressure of the electron field at the radius a is the same within the body of the electron, meaning that the charge e has an appropriate distribution conforming with this condition, then the speed of propagation of wave disturbances in the electron charge itself has the value c and that the electric energy inside that radius is e²/6a. So, you see, the net result is an electron of energy 2e²/3a giving a relationship between energy and mass that we can write as E=Mc².

Much of this was accepted physics before Einstein appeared on the scene and was known as ‘electron theory’, so it is very hard to understand how modern physicists can write that history off as if it never happened!

For our immediate purpose, we have now the basis for studying the coordinated wave interaction as between that external influence at the Compton electron frequency and the wavelengths associated with that radius parameter a of the electron.

Looking now at the figure showing the pattern of the electron’s field cavity resonance, ask yourself how the world outside the electron might interface with the world inside the core charge of the electron. If you think of pressure from the viewpoint of a gas then the interface is just a pressure interface and there is not much to say. However, a gas comprises numerous particles all moving in different directions. There are three degrees of freedom. However, inside that electron it may be that there are not numerous component particles behaving as a gas and moving with those three degrees of freedom. There could be an oscillation that has only one degree of freedom, amounting in its overall effect to a radial oscillation within the radius a. I emphasize here that I have no special insight into what goes on inside an electron. I can only make tentative assumptions and reason on that basis to see how what develops compares with what we see and measure in our experiments. So, I trust you are following the gist of my argument, because I am coming to the point that between the sphere of radius a and the sphere interfacing with those Compton frequency oscillations there is an adjustment at constant pressure in going from one degree of freedom to three degrees of freedom.

What this amounts to is that the surface area of that intermediate interface will be three times the surface area of the inner interface. In short, the outer interface radius will be 3^1/2a, subject, however, to a little ‘tuning’.

Now, if this seems a little speculative, there is an alternative approach giving the equivalent result. Look again at the figure and imagine both the radial oscillations within the core charge of the electron and in the cavity excited at the Compton electron frequency as setting up standing wave antinodes needing to balance those of travelling waves progressing by reflection around a circuit within the middle cavity. You will see that the three-wave interface at the charge surface requires a 120^o angular separation. The geometry of this system also requires the outer radius to be 3^1/2a.

A vital consideration is what it is that tells an electron that it is a negative charge or a positive charge. I do not want to dwell too long on this point so I will simply explain that it is all a question of how those the two frequency modes of oscillation beat together. Undoubtedly, as those who may study the history of aether theory may discover, the answer lies in developing the concepts of C. A. Bjerknes of the period 1877 to 1910. Positive and negative are states involving oscillations in antiphase, all positive charges sharing a common phase and all negative charges sharing a common phase, but I leave that research to others. Suffice it here to say that the phase of oscillation is important. The Compton electron wavelength has to blend with the wavelength 2a, as the reader can work out from that pattern shown in the figure.

The ratio of these wavelengths has to be an odd integer that cannot be factorized as that would allow the phase of the electron oscillations to have optional values in relation to the regulating universal rhythm of the Compton frequency oscillations. All positive electron charges have the same phase and all negative electron charges have the same phase but positive and negative charges are different because they are in antiphase.

This is the secret of the meaning of electrical charge polarity. It is just a question of phase, but there is phase-lock ensuring that there are no maverick charges in the electron family. There are only electrons or their positive versions, the positrons.

It is on this basis that there is a constraint on the adoption of the distance parameter a as a wavelength. The wavelength (λ_c) assumed by the resonant oscillation within the electron has to ensure that:

(λ_c)/2 = Na where N is a prime number.

Now, from what has been said above, it can be seen that, since a without this constraint is given by 2e²/3hν_c, hν_c being the rest-mass energy of the electron and the Compton wavelength λ_c being c/ν_c, we can write as an approximation:

a = (2πe²/hc)λ_c/3π

From these two equations we find that N becomes the nearest prime integer to 3π(137)/2, bearing in mind that α, which is 2πe²/hc, is approximately 1/137. This gives N, uniquely, as 647.

The formula for g/2 is then easily explained because the field energy of the electron disposed outside the cut-off radius R is simply e²/2R and R is simply (λ_c/2)(1+3^1/2/647). Using the formula:

(g/2)(mc² – e²/2R) = mc² where m is the normal rest mass of the electron, and also the fact that λ_c is h/mc, it then needs a little algebra to find the residual electron energy thereby effective in confined orbital states of motion. This allows us to determine its ratio to the normal energy applicable for translational motion but one then arrives at the result presented in table above.