Introduction

In this chapter we delve into the theoretical foundations of the aether itself, guided by our knowledge (a) that it comprises a uniform continuum of charge density σ permeated by charges q arrayed in a simple cubic structure owing to their mutual repulsion subject to the constraint that the electrostatic interaction energy density cannot be negative and (b) that the continuum and q charge systems, the G and E frames, respectively, are displaced 2r one from the other owing to their relative motion at speed c in circular orbits of radius r given by:

r = h/4πm_ec ……………………………….. (7.1)

The task ahead is mathematical in that we have to compute the lattice dimension d in terms of r, where d is the side of a cube of space housing each charge q. The photon will emerge as the largest symmetrical unit of that lattice structure which can spin about an axis of that structure without crashing into adjacent structure. It is also the smallest cubic unit of that lattice that has a lattice charge q at its centre. That spin involves energy and sets up pulsations which disturb surrounding lattice structure at a frequency characteristic of the energy quantum involved. Thus, in terms of the ratio of r/d, we will arrive at a formula for Planck’s constant in terms of two physical quantities pertaining to the aether, the charge q and the speed c. That dimensionless formula is known as the fine structure constant.

In the process we will have established the mass-energy of the lattice charge q, that of the quon, as well as the energy density of the aether, which will thereby indicate the mass-energy of the pair of virtual muons that exists for each cubic aether cell of side dimension d. Additionally, our analysis, by bringing the electron into the picture, will derive the odd integer value N that was introduced in chapter 2 as having the value 1843.

Such is the scope of this chapter. It is the essential foundation on which the whole of this author’s theory is founded. The analysis to be presented was developed in the latter part of the 1950s and was first published privately in printed form in 1960 in the author’s 48 page booklet entitled: ‘The Theory of Gravitation’, when the author, owing to a change in employment upon being appointed to a Senior Manager position with IBM, was obliged to arrest his private research pursuit to concentrate upon his career in the patent profession. This explains why the advancement of the theory became so protracted in development over time and lacked the endorsement which a career in academia can offer. It is a curious coincidence that Einstein’s theory was conceived during his early years as a Patent Examiner in Zurich, given perhaps the stimulus of dealing with the field of invention on a daily basis, and no doubt Einstein was lucky in finding the favour of Max Planck, who supported publication of his papers. However, in moving ahead now to publish this account of my theory, which is probably my final contribution on the subject, it is for future generations to judge the merits of my work relative to that of Einstein. Hopefully, what I have to say will have some impact, but as to this chapter 7, for my part it is more a reminiscence on past work dating back some 50 years, from when I concluded my years of Ph.D. research and entered the patent profession.

Do keep in mind, however, that I have presented something of vital importance in earlier chapters, something wholly new, by changing my account of gravitation from the interpretation of gravity as an electrodynamic force consistent with the expectations of those in search of a unified field theory to the recognition that gravity is, in a sense, an ‘inverted’ electrostatic force. The theoretical derivation of G, the constant of gravity, in terms of gravitons is unchanged, but I will explain more fully in chapter 9 the reason why I was obliged to alter course. The contest against Einstein’s theory is nevertheless as strong as ever and I hold my ground firmly in now reproducing here in this chapter 7 an edited and slightly extended version of pages 103115 of my 1980 book: ‘Physics Unified’.

The Mass of the Quon

We first consider the aether particles, the quons, that form the E frame lattice system. As with the gravitons and electrons, the Thomson formula is used to relate energy E, mass and charge radius of the quon, its charge q being the same magnitude as that of the electron:

E = 2q²/3b ………………………………… (7.2) where b denotes quon charge radius.

Quons have the lowest energy quantum of all charged particles, owing to their radius b being larger. The least energy state is justified by the fact that the lattice structure of the undisturbed aether must be the ultimate in stability, a feature which demands also that the quons must be in a state of equilibrium in their interaction with the rest of the aether system. This is assured if the energy E, as a property of a charge sphere of volume 4πb³/3, implies an energy density which is common to the aether as a whole and so shared by the surrounding medium. Thus, with d as the lattice dimension, the cube side length or spacing of the cubic array of quons, we can say that the total energy per unit cell of volume d³is:

E_o = (1/2π)q²d³/b⁴ …………………………… (7.3)

This is the energy density of the aether, on average, attributable to the notional rest-mass energy, and is deemed to be that of a pair of virtual muons as if there is one such pair in each cubic cell of aether. Such muons are active by creation and decay by mutual annihilation followed by recreation as on ever-ongoing process. This needs a little clarification concerning the interplay between the muons and the quons and so is subject to later commentary near the end of this chapter.

The effective mass of the quon is not found by using the formula E = Mc², because, when the quon moves in that uniformly dense background sea of energy, it behaves as if its mass is halved. This is akin to a known property of the motion of a spherical body through a liquid. We know from the study of hydrodynamics that, if that body has a mass density equal to that of the liquid, it seems weightless owing to buoyancy, but there is an apparent increase in mass when a sphere is accelerated as if that mass is half of the true mass of the body.

We proceed by accepting that this analogy applies to the problem of the aether and so our lattice particles will exhibit an effective mass in their orbits of radius r of:

m_o = q²/3bc² ……………………………… (7.4)

The lattice particles, the quons, mutually repel by their Coulomb interaction. As in the formation of crystal structure within matter, we may then expect some kind of cubic or hexagonal lattice to form. This is the minimum energy structure that applies in the circumstances, but those circumstances as they exist in matter are quite different from the situation in the aether, because the minimum energy criterion in matter usually results in what is an overall negative energy density. This is because the omnipresent aether has a slightly positive energy density and so it can permit matter to exist in a crystal structure that the aether is denied owing to the fact that its minimum energy density attributable to electrical interaction has to be positive.

I then found, from my analysis of the aether, that if minimum energy conditions were applied to the space medium and negative energy density were to be permitted, then the aether lattice particles would all be at rest at neutral positions in that charge continuum, each quon sitting in its own cell and in a structure that was body-centred cubic, as in iron. There would be no motion. Our universe would be dead and lifeless. The aether would have no character relating to time and the exercise of exploring its properties would be meaningless.

However, by assuming that the lattice particles of the aether would form in a structure which involves the least possible electrical interaction energy consistent with it being everywhere positive, then, Eureka, everything fell into place. The aether lattice structure had to be simple cubic in form. There had to be displacement of the particles from the centres to which they were drawn by electrostatic action and, to keep that displacement, they had to move in orbit in synchronism with one another and so the aether became a clock which keeps perfect time, even though it ticks at the very high frequency we associate with electron creation.

It has been shown in chapter 6 that the charge displacement distance is 2r, where r is the radius of the orbits involved, and that the angular speed Ω in orbit is c/2r. Presenting again the electrostatic force expression (6.1) of that chapter and equating it to m_o(Ω)²r, we have:

m_o(Ω)²r = (4πσq)D ………………………… (7.5) where D is 2r, which gives us an energy term: m_oc² = 32πσqr²………………………….. (7.6) Since the space medium is electrically neutral:

q = σd³ ……………………………….. (7.7) This brings us very close to obtaining a value of the quon mass in terms of r/d and the unitary charge e of the electron, presuming that q is equal to e, and so the onward task now is to determine the value of r/d.

The Aether’s r/d Factor

This ratio r/d, as the orbital radius r of the rhythmic quantum jitter motion of the aether in terms of the aether lattice cell dimension d, is determined as being very slightly greater than the r/d value at which the charge q interacts with the continuum charge density σ to have zero electric interaction potential.

Accordingly, the governing equation is:

E = _∑∑( q²/2x) –_∑∫(qσ/x)dV + _∫∫( σ²/2x)dVdV

………….. (7.8)

The factors 2 in the denominators are introduced because each interaction if counted twice in the double summation and double integration. The summations and integrations extend over the whole volume of space but as we shall see it suffices to limit the range to just a few lattice spacings d. To simplify the presentation we regard d as unity in the stages of integration and summation. Boundary conditions are of little consequence. Electric interaction energies, when reduced to local energy density terms, can in no way depend upon remote boundary conditions. The lattice condition assumed need not hold as a rigid perfect lattice throughout space. It can be distorted, but we do not expect the synchronous character of the lattice particle motion to hold beyond the range of the boundaries of vast space domains of the aether, domain size being a matter of analysis in chapter 8.

The next step in our analysis is to differentiate E of this

equation (7.8) with respect to σ, after recognizing that _∑∫(qσ/x)dV

incorporates an offset term 2πσq(2r)² to allow for the 2r displacement. The object of this is to eliminate the σ-σ interaction by determining the minimal energy condition by equating the result to zero. Then we shall know that distance 2r.

Differentiating (7.8) with respect to σ, equating to zero and then multiplying by σ, we obtain:

_∑∫(qσ/x)dV = _∫∫( σ²/x)dVdV ……………. (7.9)

From (7.8) and (7.9) we then find that:

E = _∑∑( q²/2x) –_∑∫(qσ/2x)dV ……….. (7.10)

Since E is zero the factor 2 is not important as we now evaluate the relevant terms in five stages and consolidate the results in a sixth stage.

Stage 1:∑( q²/x) between one quon and surrounding quons Still regarding d as unit distance, the coordinates of all surrounding quons in a cubic lattice are given by l, m, n, where l, m, n may have any value in the series 0, and plus or minus 1, 2, 3, etc. with the co-ordinate 0,0,0 excluded. Consider concentric cubic shells of surrounding quons. The first shell has 3³-1 particles, the second 5³3³, the third 7³– 5³, etc. Any shell is formed by a combination of quons such that, if z is the order of one shell, at least one of the co-ordinates l, m, n is equal to z and this value is equal to or greater than either of the other two co-ordinates. On this basis it is straightforward arithmetic to verify the following evaluations of this sequence of summations. S_z denotes the summation as applied to the z shell. S₁ = 19.10408 S₂ = 38.08313 S₃ = 57.12236 S₄ = 76.16268 S₅ = 95.20320

By way of example, S₂ is the sum of the six terms: 6%4 + 24/%5 + 24/%6 + 12/%8 + 24/%9 + 8/%12 and here 6+24+24+12+24+8 is equal to 5³– 3³.

Stage 2: The evaluation of _∫(qσ/x)dV in relation to S_z

The limits of a range of integration corresponding with the z shell lie between plus or minus coordinates (z -1/2) and plus or minus coordinates (z+1/2). An integral of qσ/x over these limits is denoted qσd²I_z where:

1

I_z = 24z _∫( sinh^-1[1+y²]^-1/2 )dy

0

which, upon integration, is: I_z = 24z(cosh^-12 -π/6)

and which, upon evaluation, is: I_z = 19.040619058z ………………………. …… (7.11) Note that within I₁ there is a component I₀ for which z in this latter expression is effectively 1/8 so that: I₀ = 2.380077382 ……………………………….. (7.12)

Stage 3: _∫(qσ/x)dV for quon 2r displacement

As already indicated this component of the integral is given by: 2πσq(2r)² and this expression, in units of q²/d, with σ as q/d³ is, simply:

8π(r/d)² ……………………………………… (7.13) and so, once we merge the results of stage 1 and stage 2, we are close to determining the value of r/d from their difference.

Stage 4: Correction for quon charge volume

The stage 2 calculation did not allow for the physical displacement of σ charge owing to the finite size of the quon, which has a charge radius b. This correction term is the integral from 0 to b of σq/x as it applies within a spherical shell of area 4πx² and thickness δx. This is:

2π(b/d)²(q²/d) ……………………………….. (7.14) and, from (7.4) and (7.6), we know that:

b/d = (d/r)²/96π ……………………………. (7.15) so that, in units of q²/d, the correction found by combining (7.14) and (7.15), is:

(d/r)⁴/4608π ………………………………….. (7.16)

Stage 5: Combination of terms.

One very minor term is still needed to complete the analysis. This is because the quons, along with any particles of matter that sits in the E frame, will be moving relative to the charge continuum σ at the relative speed c and this must drive the σ charge out of their way and so compress σ to a moderate extent. It would seem appropriate to accept that the mutual repulsion within the σ charge owing to this compression will spread the effect over a relatively large region so as to minimize the energy needed, energy which will add in some measure to the σ-σinteraction.

Because the volume of continuum charge displaced by the presence of a quon is very much greater than that displaced by protons and electrons, this consideration is a factor needing consideration only in respect of the quons.

We proceed by estimating its significance in relative terms as referenced on the quantity defined by (7.16) as just derived. The charge displaced by the quon is 4πb³σ/3 and its displacement is to a mean distance kb, where kb can have a value approaching d/2 if the displaced charge is spread over much of the aether cell, would imply an energy term given by:

4πqσb³/3kb which is: (4π/3k)(b/d)²(q²/d) ……………………………. (7.17)

This is 2/3k times (7.14) and so, since (7.16) was derived from (7.14), the result we seek is the factor 2/3k which must be small owing to the self-repulsion of σ but yet must not be less than 4b/3d.

Stage 6: Consolidation of results

We now need to find the difference between the summation of the S terms and the summation of the I terms. Their convergence is self-evident. Ignoring I_o for the moment, the successive terms differ by a summation of the terms:

0.06346 + 0.00189 + 0.00050 + 0.00020 + 0.00010 …. and, to sum the series, we match it to: 0.01350[1/3³ + 1/4³ + 1/5³ + 1/6³ …….] or: 0.00050 + 0.00021 + 0.00011 +0.00006 …..

for terms from z = 3 onwards. This yields the summation 0.00105, which upon adding 0.06346 and 0.00189, gives 0.0664 to subtract from the I₀ quantity of (7.12) to obtain 2.31368.

This value is the number of units of energy q²/d that we derive per quon from the first two stages of this analysis. The third, fourth and fifth stage components are now combined to give the net zero energy quantity and leave us with the equation:

8π(r/d)² = 2.31368 -(1 -2/3k)(d/r)⁴/4608π ……… (7.18)

This is the equation we seek, because it allows us to obtain a very close estimate of the value of r/d. Ignoring the term involving k, r/d is found to be 0.302873.

Now, before considering that k term, it is appropriate here to mention that I am indebted to certain independent initiatives taken by three individuals, including one in particular, who have put in a great deal of effort to verify the analysis I have presented here. The first such initiative was that of Peter N. McNeall, an Englishman living in USA, who drew my attention to a small numerical error in a version of this analysis presented in the 1966 edition of my book: ‘The Theory of Gravitation’. The second and most important contribution was that of another Englishman, Dr. D. M. Eagles, who, having seen my 1969 book: ‘Physics without Einstein’, met me to discuss what it claimed, whilst in U.K. between a relocation of his research employment in USA to the National Standards Laboratory in Australia. I mentioned him in chapter 2, when I referred to a table in a book by B. W. Petley where Petley had drawn attention to a paper which Dr. Eagles and I had jointly authored. This paper was the result of Dr. Eagles checking my manual efforts at analysis to compute r/d in the days when powerful computers were available only to scientists in major research facilities. With Dr. C. H. Burton’s assistance at that Australian laboratory he produced the definitive result of such a calculation by using such facilities and duly advised me that r/d obtained by such analysis was 0.302874.

Precision here was very important owing to the implications this had for determining, with a high degree of confidence, a numerical quantity which seemed, by coincidence, to be close to the proton-electron mass ratio but yet was somewhat higher. I refer here to the number N that was introduced earlier.

As to the third independent initiative, which has greatly impressed me, it is that of Bill Buick, of an address in Scotland, who went to the trouble of providing a computer program which anyone can run on a home computer to give the results of the calculations involved in deriving r/d.

In summary, therefore, since the whole of this aether theory hinges on the calculation of this quantity, I am able to assure readers that the analysis is sound and meaningful. We can, therefore, now proceed to the more interesting features of this work by deriving that quantity N that is key to the three constants of Mother Nature that we are decoding.

Evaluating N

We define N as the ratio of the charge volume of the quon to that of the electron. We shall examine the proposition that N must be an odd integer, simply because the quon is not only the ultimate decay product of an electron but is, as we have seen in chapter 4, the seat of birth of the proton, which implies input of sufficient energy to create a number of electrons and positrons that can coalesce to form the proton by shedding a little energy. We can, therefore, expect N to be of the same order as, but higher than, the proton-electron mass ratio.

If we focus attention now on the photon unit we described in chapter 6 and take note of a topic discussed separately in Appendix II, the picture before us is that of a 3x3x3 cubic section of aether lattice being able to spin within enveloping aether lattice. Here we have a kind of spinning crystal formed by 27 quons of which 24 account for the quantum of angular momentum.

Referring now to Fig. 7.1 it will be seen that a circle is drawn to depict a sphere which encloses those 27 quons seated at the lattice sites in the cubic array there depicted. The radius of that circle is 2πr. Why is this? Well, we have just seen that r/d has a value of 0.302874, so 2πtimes r will be 1.903d, which is the basis on which the figure is drawn.

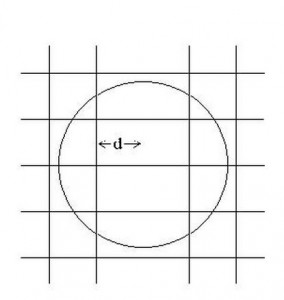
Fig. 7.1

From chapter 6, reproducing equation (6.20):

I = 2h/πΩ …………………………………. (7.19) we know, because Ω is c/2r, that this term I, now representing a moment of inertia, is:

I = 4hr/cπ ………………………………….. (7.20)

The moment of inertia of the 3x3x3 lattice, as we see from inspection for spin about a 3-quon axis, is 36m_od², because there are twelve quons distant d from the spin axis and 12 quons whose square of distance from that axis is 2d². Equating this result to I then gives:

36m_od² = 4hr/cπ …………………………… (7.21)

Now, having regard to equations (7.6) and (7.7), we see that these combine to give: m_oc² = 32π(q²/d)(r/d)²……………………… (7.22) and we can here once again restate equation (6.15):

r = h/4πm_ec ………………………………. (7.23) to give us three equations which, in combination, can, by a little algebra be seen to yield two further equations:

hc/2πe² = 144π(r/d) ………………………….. (7.24) and: m_o/m_e = (4/9)(r/d)²………………………….. (7.25) Note that e, the unitary charge of the electron, now replaces q, as the two are identical.

We are now ready to determine N because the ratio of the two masses in (7.25), as multiplied by 2, is the inverse ratio of the charge radii of the electron and quon. This factor 2 arises because the effective mass of the muon in its aether E frame orbits is half that determined from the Thomson energy equation.

We then establish that N, as the ratio of the quon charge volume to that of the electron, is given, from (7.25), by: N = (9/8)³(d/r)⁶ ……………………………. (7.26) which, with r/d as 0.302874, gives N as approximately 1844.53.

This, however, is not allowing for that stage 6 correction mentioned above, nor are we taking into account that requirement that N is an odd integer, integer because the quon has to be able to transform by energy addition into a group of electrons and positrons and odd because charge parity has to be conserved.

From equation (7.18) we see that the effect of that term involving k is to increase r/d slightly. This will decrease N. We seem therefore to be looking at a definitive value of N that is 1843, but let us just explore this by working (7.18) backwards to see how large k must be to ensure that we do not slip below this 1843 threshold as an integer value. This is when r/d has the value 0.302916 and k is 8.34.

We can now proceed by first noting that equation (7.24) represents one of the numbers we set out to decipher, namely the fine structure constant. You can then check that an approximate value of r/d of 0.302916 will give the constant as quite close to the measured value of 137.0359895(61). Then note that the value of b/d is known from equation (7.15) as:

b/d = (d/r)²/96π which allows us to estimate the significance of that factor k. We find from the above value of r/d that b/d is 0.035 and so the distance kb, with k as large as 8.34, tells us that the charge displaced by the quon must move away from the quon centre by a mean distance of more than 0.29d in order for the energy conditions to be consistent with the 1843 value of N rather than a lower value of 1841. This seems an ideal requirement, given that the σ charge displaced in the continuum will try to spread itself owing to its self-repulsion, but yet must be confined within the boundaries of a cubic cell of side dimension d.

Accordingly, we have now arrived at the conclusion that N is 1843 and, this being a key factor in this theory by which we decipher Nature’s coded messages, we have accomplished the main task of this work. The fine-structure constant, as expressed in reciprocal form by equation (2.10) in chapter 2, has been derived, as can be seen by combining equations (7.24) and (7.26) to eliminate the ratio r/d. One remaining task, before we embark on the quest to explain how stars are created, is to justify the value of the energy E_o of a unit cell of space, this being the energy quantum we have assigned to the two virtual muons which live within each such cell.

The Unit Energy Quantum of the Aether

The relevant equation is that presented in the early paragraphs of this chapter, namely equation (7.3), which is: E_o = (1/2π)q²d³/b⁴ This, plus the equation (7.15) just quoted above, combine to give: E_o = (1/2π)(96π)³(r/d)⁶q²/b …………………….. (7.27)

From (7.26) this becomes:

E_o = (3/4π)(108π)³(1/N)(2q²/3b) …………….. (7.28) which presents this energy quantum in units of the quon mass-energy according to the Thomson formula. The latter is the electron rest-mass energy divided by the cube root of N and so we obtain:

E_o = (3/4π)(108π)³(1/N)^4/3 m_ec²……………………. (7.29) from which we find, with N as 1843, that this energy quantum becomes:

412.6658 electron rest-mass energy units. Here, then, is the energy quantum that is regarded as the virtual muon pair, the occupants of each cubic cell of aether.

A Supplementary Note

My object in this chapter 7 has been to present the analysis by which I did, during a period in the latter part of the 1950s, work out what had to be the necessary structure of the space medium, the aether, in order for it to determine the processes we refer to as quantum theory and gravitation. I did not in those early years have an adequate insight into the details underlying the creation of the proton or the graviton, but their basis of existence was clear and the picture came fully into focus with the passage of time, the g-graviton emerging first, in the mid 1960s and the proton by the mid 1970s.

Admittedly, however, there remain unanswered questions, questions that may elude us for many generations to come, some forever. There is scope for others to address these problems and add to our enlightenment.

A typical question is: “How can it be that a fundamental particle having an electric charge e confined within a sphere does not expand indefinitely owing to the self-repulsion of its electrostatic charge?” Can the answer lie in the rhetorical question: “Well, owing to its spherical symmetry, it has a centre and, since that is also its centre of mass, if it were to expand and shed energy, meaning what can only be kinetic energy, then what would determine the direction in which that centre of mass would move?” Should we beg the question, as it were, by arguing that the charge is stable because it cannot move of its own accord and allow its energy to become kinetic energy?

Another such question is: “What is it in Nature that tells an electric charge it is positive or negative?” Here, the answer could be in our awareness that electric charge forms tend to be created in pairs and with two fundamental particles of opposite charge one can visualise one expanding as the other contracts so that energy is exchanged between them without having to convert into kinetic energy. This is a picture of mutual stability enhancing particle lifetime, and suggesting a well-known saying that there is ‘safety in numbers’. The idea thus seeded is the notion that all electric charged particles are oscillating in their charge radius at a common very high frequency, probably that of the quantum motion of the E and G frames of the aether, and that whether a charge is positive or negative really depends solely on its phase of oscillation. To accept that you must accept that time, as set by the rhythm of the quantum underworld, is universal and governed by motion that is synchronized as if there is no retardation in the action. That may seem a debatable proposition, but it makes sense for conditions where there is no need for long range energy transfer.

Before concluding this supplementary note to chapter 7, I will now raise and seek to answer three questions which mayalready have occurred to astute readers. Why is it that it is so important for the electrostatic interaction energy of the aether not to fall below zero, given that when two electric charges of opposite polarity do interact there has to be a negative energy component offsetting the self-energy of each charge? The answer lies, I believe, in the lack of reciprocity in the charge interaction combined with the fact that no vector direction is defined that can give scope for kinetic energy. If two charges of different electrical polarity but identical form interact then energy exchange can occur and even if of different form there is a line between their charge centres along which the charges can move apart as any surplus energy is shed to become kinetic energy. This is not the case for those quons sitting in a charge continuum σ. It is just as well, because if the quons were to move to sites of minimum electrostatic interaction energy, meaning a negative energy density as offset by the self-energy of the quons, then the aether would be a solid devoid of any motion and we would not exist.

The second question arises when we note how precise the aether analysis has been in defining numerical relationships but see an approximation in taking E_o as the total energy of a cubic cell of the aether, as if the quon is part of the virtual muon pair when it comes to using E_o as in the calculation of the proton-electron mass ratio in chapter 4. I answer this by saying, or rather hoping, that the ongoing creation and decay of those muons as they deploy from position to position in the aether will occur as if they have just such a spacing as to account for a negative interaction energy that exactly matches the positive energy of the quon and its equal measure of associated graviton energy. However, there may well be another answer, one bearing upon the inseparability of the quon charge from its counterpart continuum charge of opposite polarity.

The quon with its matching unit of continuum charge is the most degenerate state that electric charge can adopt. Hence the quon, unlike the electron, may find that its electric field energy is somehow merged with and perhaps accounts for energy that represents the presence of that continuum. Note that the theory assumes the continuum proper has zero energy. We should not therefore expect the inertial properties of the quon to be the same as those of the electron, as implied by use of the Thomson mass-energy formulation E = 2e²/3a. Now here I have in mind what I wrote at pages 104-105 of my 1969 book: Physics Unified. I argued by reference to Appendix I of that book that the pressure in the medium enveloping the quons would be equal to that set up within the body of charge e, which I calculated as being given by the formula e²/4πa⁴. From this, by multiplying by the volume of a sphere of radius a, one can obtain a measure of the energy as e²/3a, which is half that given by the Thomson formula.

A little intuition then leads to the appealing suggestion that the continuum counterpart to such a quantity as applied to the quon might then account for an equal amount of energy, so bringing their combination to the energy quantum that would apply to the quon by use of the Thomson formula.

The latter concern may point to a weakness in the theory but only in the sense that one surely cannot expect the universe to yield all its secrets and be self-explanatory in every detail to fit within the pattern of this one sweeping account of Creation. One can but probe the aether step by step and I must admit that I have no idea how to explain or justify the existence of the continuum of charge density σ, nor can I say what electric charge actually is other than by describing its action and effect on other charge. This gives rise to the third question. What happens if, instead of the charge continuum yielding to compression owing to the motion through it of quons and matter at a relative speed c, it resists compression and stays uniform, but the quons are compressed to match exactly the volume of space taken up locally by the particles of matter? This would eliminate the need for that factor k in stage 5 above and ensure that the presence of matter does not distort the continuum charge distribution as a function of the volume of matter particles involved, meaning that gravitational interaction is exclusively that of the related graviton presence.

The results of our analysis speak for themselves, but I do not have the slightest notion of how electric charge can spread itself to fill space in a uniform way, short of imagining that in its microcosmic form it is like a gas which somehow disperses uniformly in its pressure balance.

We can, however, build on what has been discovered concerning the aether and this takes us into chapter 8 where we will see how stars are created.