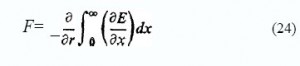1

Unified Field Theory

 

The Challenge of the Unified Field

On September 10, 1948, Albert Einstein wrote a foreword for a book[1] by Lincoln Barnett entitled “The Universe and Dr. Einstein”. This foreword concluded with the words:

The growth of our factual knowledge, together with the striving for a unified theoretical conception comprising all empirical data, has led to the present situation which is characterized-not with standing all successes-by an uncertainty concerning the choice of the basic theoretical concepts.

Quoting from the 1966 edition of this work, one reads:

Dr. Einstein, long professor emeritus at the Institute for Advanced Study in Princeton, spent the last years of his life working on a problem which had baffled him for more than a quarter of a century. This was his Unified Field Theory, which attempted to set forth in one series of mutually consistent equations the physical laws governing two of the fundamental forces of the universe, gravitation and electromagnetism…. ‘The idea that there are two structures of space independent of each other, the metric-gravitational and the electromagnetic,’ Einstein once observed, ‘is intolerable to the theoretical spirit.’ Yet despite all his efforts he could not incorporate electromagnetic field laws into General Relativity.

Today, as we progress through the 1980s, the pursuit of a viable Unified Field Theory is as elusive as ever. One might well question whether the quest defies solution. Perhaps we have been wrong to prejudge that unification of electrodynamic and gravitational force relationships will emerge from analysis relying strictly on the field concept.

Note that in the above quotations Einstein did not use the word ‘field’. Those involved in the early study of electrodynamics were very careful to treat their subject empirically, guided by measurements of interaction forces between currents in closed electrical circuits. The concept of a field was merely a consequence of the theoretical interpretation of a restricted range of experimental data. There were no measurements of the electrodynamic interaction forces between discrete charged particles in motion.

Certainly, the electric field associated with the electrostatic interaction formulated in Coulomb’s Law, though only notional, seems real enough, because the lines of flux portraying the electric field radiate from the electric charge. However, the notional magnetic field lines we associate with moving charge form closed loops in space remote from the charge itself (see Fig. 1). One should, therefore, be a little less confident as to the reality of such fields in the surrounding void.

 

Figure 1

Nevertheless, the overwhelming success of Maxwell’s work on field theory and the fact that Maxwell’s equations stand firm under relativistic analysis have secured confidence in the universality of the field concept. The Special Theory of Relativity has been accepted as a unification of field theory so far as electricity and magnetism are concerned and this leads us to hope that the remaining challenge of discovering the onward unification with gravitational theory will emerge from research involving relativistic field concepts.

Be this as it may, the fact that others have been unable to find the connection has led the author to explore an avenue along different lines. It seems best to make a detour around the field concept and concentrate on the unification of electrodynamic and gravitational force relationships, without reference to fields. The problem is rather formidable, for two reasons. First, it requires us somehow to relate Newton’s direct inverse-square of attraction law of gravitation with a law of electrodynamics which does not, in general, give force acting directly along the line between two interacting charges. Second, we have to seek unification, not with the simple law of Isaac Newton, but with the more complex law of gravitation deduced from Albert Einstein’s General Theory of Relativity. Einstein’s law of gravitation does, however, give a force along the line joining two interacting bodies.

Our object in this chapter is to show first how the electrodynamic force can be formulated on the basis of experimental data so as to be compatible with Newton’s Law of Gravitation. Also, we will explore an aspect of inverse-square laws in general, which will allow us to encompass Einstein’s law of gravitation. A unification of form between electrodynamics and gravitation will emerge in Chapter 2. Then, given this, the task of justifying a physical link between electrodynamics and gravitation comes into sight and with it the broader objectives of this book, a more unified account of fundamental physics.

The Electrodynamic Force

Merely by taking full account of the conservation of energy there are certain general aspects of the force which acts on a charged particle in motion, bearing in mind that the force is taken to be directed according to the polarity of the charge and the velocity of the charged particle.

Referring to Fig. 2, imagine two electric particles of charge q, Q and mass  M moving at constant velocity v, V, respectively and subject to a mutual force F acting directly between them along their

 

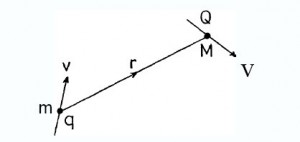Figure 2 – The Electrodynamic Force

line of separation. r is the separation distance vector from q to Q. Note that we intend to make no reference to the magnetic field as portrayed by the closed lines encircling the velocity vector v of the charge q in Fig. 1. Consider next the energy deployment as charge Q moves under the action of a force F acting in the direction -r. This is depicted in Fig. 3. Note that force is itself a concept, when considered alongside truly physical parameters such as energy, mass, distance and time. Force is merely a manifestation as energy is transferred with the changing state of a system. Without energy transfer there is no force,

F

because force in this constant velocity situation is a rate of change of energy with position.

If the interaction depicted in Fig. 2 is considered as exclusively electrodynamic, meaning that the two velocities v and V are both constant, there are certain constraints on the electrodynamic interaction force. We cannot have the charge Q moving at a constant velocity V solely under the action of force F. The force F expends work at a rate expressed by the scalar product (F.V) and the energy has to go somewhere. We might expect V to change, but we are considering what has to happen if V does not change, that is the circumstance prevailing if there are energy transfer processes at work within the electrodynamic system itself.

Clearly, if force is a consequence of energy seeking a home to assure conservation, Nature asserts another force on Q. Denote this force Z, as shown in Fig. 4. We then know that:

Equation 1 – energy transfer processes at work

The interesting point we now focus upon is that, whereas Facts through the centre of gravity of the two-body system formed by q and Q, the force Z must exert a turning moment on Q about the centre of gravity. Z cannot act through this centre because, if it did, then to

Satisfy (1). It would merely cancel F completely and then there would be no electrodynamic action to consider.

Now, as with any self-contained electrodynamic system, we know that the two-body system q, Q cannot acquire angular momentum by virtue of its own self-interaction. This is well established and applied, as will be described later in this work, in interpreting the measurement of gyromagnetic properties in magnetized pivotally-mounted rods when the direction of the intrinsic ferromagnetism is reversed. Angular momentum is conserved as between the rod and the electron motion to which the ferromagnetic state is ascribed.

Historically, there was an experiment in which self-action of currents in a closed circuit was taken to cause rotation. * Writing about it, its author Gore (1875) commented:

These experiments produce a striking effect in a lecture, because rotation appears to be produced without reaction of the moving parts of the apparatus upon any external or fixed body.[2]

Professors Maxwell and Stokes are, however, on record as having challenged Gore and pointed to a weakness in his experimental setup. Once remedied, the effect did not occur. Hence, the inability of an electrodynamic system to develop rotation by self-action is fundamental and well accepted.

To balance the turning action of Z there has to be a third force acting on Q. This third force P is an extraneous force arising by reaction. As is usual with reactionphenomena, the reaction force is that associated with a maximization of energy transferred, corresponding to a minimization of potential energy in the primary action. Thus, for optimum reaction involving maximum energy transfer as Q is displaced, the force P has to be in the line of the velocity vector V.

 

So, our argument about energy exchanges and balance leads us to imagine that there are three forces acting on both q and Q, as depicted in Fig. 5. The counterparts of Z and P at q are denoted Z’ and pi, respectively.

 

 

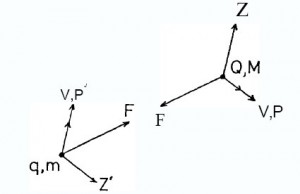
Fig. 5, as drawn, now suggests the most important step in this analysis. We are seeking to explain electrodynamic action as a direct interaction along the lines joining q and Q, that is, solely in terms of

F. Yet we know that this primary action is complicated by reaction forces Z, P, Z‘ and P‘. What is the condition that the separation vector between q and Q should be unaffected by the motion of the system in response to these four reaction forces? The answer simply is that Z and P must combine to assert a force on M that accelerates it exactly as m is accelerated by the combination of Z’ and P’, and these four forces must assert no turning couple on the system. The fact that the electrodynamic self-action produces no turning couple is a consequence of the basic requirement that the separation vector r is governed solely by the mutual electrodynamic interaction force F.

When formulated, the condition just deduced leads to:

 

Z = (M/m)P’    (2)

and

Z’=(m/M)P       (3)

And Z is parallel to pi and Z’ is parallel to P.

If we knew F, we could, from (1), (2) and (3), derive the complete law of force applicable to the interaction between q and Q. The derivation of F is, therefore, the next task.

The Neumann Potential

The electrodynamic action is characterized by a reversal of force when the current of either interacting circuit element reverses. Also, as was known to Ampere as long ago as 1825, the electrodynamic forces exerted by one circuit on another are independent of the linear dimensions of the circuits and so, from dimensional analysis, the force must vary as the inverse-square of separation distance. For an interesting commentary on this see the book by Tricker (1965)[3].· These facts alone allow us to deduce the form of the electrodynamic interaction force F.

The system of the two charges q, Q shown in Fig. 2 can be resolved vectorially into nine component interacting systems, with r drawn along the x axis in an x, y, z set of co-ordinates. Thus each of the components Vx, Vy, Vz of velocity, interacts separately with each of the components Vx, Vy, Vz of velocity V.

There are four types of interaction and we consider each below.

 

Firstly, the action for which the two velocities are mutually orthogonal and one lies along the separation vector, as shown in

there is a mutual balanced interaction force acting between q and Q then it must reverse in direction if the velocity of Q reverses. Yet if the velocity of Q reverses we have but the same system when viewed in reverse direction from behind. Accordingly, by symmetry, the force cannot reverse and so must be zero, since we know it has to be proportional to the velocity if it exists at all.

Secondly, the action for which the two velocities are mutually orthogonal and orthogonal with respect to the separation vector, as shown in Fig. 7. The velocity of q is directed normal to the plane of the figure.

Here, if there is mutual balanced interaction force between q and Q then a related potential energy will be associated with the state depicted in Fig. 7. This energy should be the same however the state comes about. It will be proportional to the product of the two velocities in the state shown. Imagine that q travels at high speed and Q at low speed, to create the state in Fig. 7. During its travel q has velocity components, one of which is orthogonal to the separation vector and the other of which is directed along the separation vector. Motion orthogonal to the separation vector involves no work against

the mutual force deemed present in the Fig. 7 system. Motion along the separation vector involves no work because we have seen that the force is zero in the Fig. 6 system. Hence no work is expended in creating the Fig. 7 configuration from two well-separated charges. It follows that the electrodynamic interaction depicted in Fig. 7 has no energy and that there is no force between q and Q.

The above argument is more readily understood by reference to Fig. 8, which depicts the charge q progressing rapidly in a direction orthogonal to the motion of Q, the latter being directed normal to the figure. Note that if we were considering current flow along circuit elements, the circuit could be configured as drawn in Fig. 8.

 

 

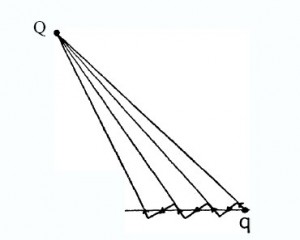
As can be seen, segments along the flow path of q correspond alternately to systems of the kind shown in Figs. 6 and 7, respectively.

The third action is that depicted in Fig. 9 and the fourth that shown in Fig. 10. The problem is that of relating the mutual balanced interaction force deemed present in the two systems. Let the force in

 

Fig. 9, measured in the mutually-attractive sense, be taken as aqQvV  at unit spacing and the force in Fig. 10 as bqQvV at unit spacing. Apply these expressions to the charge configuration shown in Fig. 11.

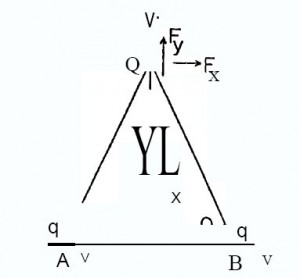
Here charge Q moves very rapidly at a velocity V away from a symmetrical system of two charges q moving laterally at velocity v in the same plane. Let the force on Q attributable to the combined effect of q at A and q at B have components Fx and Fy as shown. The force Fx does no work, inasmuch as Q moves in the directiony. The forces Fx and Fy are each the sum of four force components based upon a resolution of each of the q-Q interactions into two of the systems of the form shown in Figs. 9 and 10. Interactions of the form shown in Fig. 6 have been ignored, since the interaction force has been shown to be zero.

It may then be verified that, taking the q-Q spacing as unity:

Fx=qQvV{(b-a)cos²8sin8 +(b-a)cos²8sinB}    (4)

Fy=qQvV{(b-a)cos8sin²B-(b-a)cosBsin²8}  (5)

Evidently, Fy is zero. Also, since Fx does no work either, then the electrodynamic potential of the system is independent of the presence of Q. This means that the electrodynamic forces on the charges q arising from Q must equally do no work. Yet the force –Fx acts in opposition to the motion of the q charges and is shared between them. If this force is finite work must be done as the charges q travel at velocity v. Clearly, therefore, we must conclude that Fx is also zero. This necessitates acceptance that a=b. In other words, the interactions of the systems of Figs. 9 and 10 are identical.

Reverting now to the analysis of the general interaction shown in Fig. 2 and the nine interaction components in the resolved system, we find that six of these arezero interactions of the form shown in Figs. 6 or 7. One is of the form shown in Fig. 9 and two have the form shown in Fig. 10. The total interaction force, expressed in the resolved velocity components, is:

Since this force is an attractive force, by assumption, and is acting along the line of the separation vector I, we can write (6) in scalar product notation, thus:

F =-aqQ(v.V)rjr³       (7)

If this is written in current element form by putting QV=ids and qv =i’ds’ and a is put as unity, this expression becomes, when integrated as a potential, the Neumann Potential:

-ii'(ds.ds’)jr      (8)

This is the classical energy potential associated with the electrodynamic action. I and i‘ denote currents in circuit elements ds, ds’ separated by a distance r. The fact that two parallel current circuits mutually attract when the currents flow in the same direction determines the sign of the expression and justifies the assumption that a is positive. The unity value of a is merely set by the choice of units.

Having established the form of the force F, we are now ready to formulate the full law of electrodynamics. Write F as:

F =-K(v.V)r             (9)

where:                             K=qQ/r³                (10)

From (I) and (9), the force Z in Fig. 5 is given by:

-K(v.V)(V.r) +(Z.V) =0

Hence:      Z=K(V.r)v                        (11)

Conversely, bearing in mind that F acting on q is reversed:

ZI= -K(v.r)V   (12)

From (3) and (12):

p=-K(Mlm)(v.r)V   (13)

 

The total force acting on Qin Fig. 5 is, therefore, F + Z +P, which is, from (9), (10), (11) and (13):

FQ=(qQjr³){(V.r)v–(Mlm)(v.r)V-(v.V)r}       (14)

This is the complete and general law of electrodynamics to which we have been led by straightforward analysis. It will form the basis of the unified field approach presented in this work.

 

Electrodynamics has developed empirically from the measurement of interactions between electrons moving at low speeds in closed current circuits. If we put M =m and q = Q in (14) to signify action between identical charge carriers, the law simplifies. It reduces to a simple inverse-square law of mutual attraction for actions between like polarity charges moving mutually parallel. Then the first two terms in (14) cancel to leave the last term in the simplified form:

F=-(q2/r3)(v.V)r    (15)

This establishes the form of law we seek for correspondence with Newton’s Law of Gravitation. But is the electrodynamic law, as applied to electron flow in circuits, viable?

 

The answer to this is that it simply has to be, because we have relied upon the principle of energy conservation in deriving it, and little else. To establish that we are correct, let us digress into the history of the subject.

During the course of the nineteenth century the interaction of currents in electrical circuits was fully explored. The idea that such interactions were collective effects of charged particles, all interacting in some way, was well in evidence. Even though the electron was not isolated for direct measurement of its behaviour in a magnetic field until late in the century, the theory of electricity and magnetism recognized the need for a law of electrodynamics between two isolated charges. We see Maxwell in his great treatise discussing the force which one isolated current element exerts on another.

He presented the most general law of electrodynamic action consistent with the experimental facts. The problem was to formulate the effect of a current i‘ in a circuit element ds’ upon a current i in a circuit element ds. He deduced that the general law would have three components. With r as the separation distance between two elements, his formulation showed that there was a primary force along this line joining the elements and two components of force, one parallel with ds and one parallel with ds’.

The only uncertainty arose because the experimental data invariably included a closed circuit current and this left one parameter (Maxwell termed it Q) uncertain. All he knew was that Q was a function of the separation distance r. Quoting from the third edition of the treatise (Maxwell, 1891)[4]:*

Since the form and value of Q have no effect on any of the experiments hitherto made, in which active current is always a closed one, we may, if we please, adopt any value of Q which appears to us to simplify the formulae.

Now, surely, Maxwell was not here saying that the law of electrodynamics can be left to arbitrary choice. He was saying that temporarily, until the future gives us clarifying experimental evidence, we can get by by any convenient choice of Q. Therefore, in the meantime, we may just as well make life easy for ourselves and choose a value for Q which simplifies the formulae. The Biot-Savart version adopted by Lorentz has proved to be the easiest to use. It is a twostage force relationship linking the two current elements by a common magnetic field parameter. It may be formulated thus:

H = i‘ʃs‘{lfr³)[ds’.r]         (16)

F =i[ds.H]                      (17)

However, this vector product version relating field H and force F was not suggested by Maxwell. He recited four alternative choices of Q, one which gave the law of Ampere, one which gave the above law in quaternion form (Grassmann’s law) and two of his own making. After presenting them he opted in favour of Ampere’s version, even though this was more complicated, because it was:

undoubtedly the best, since it is the only one which makes the forces on the two elements not only equal and opposite but in the straight line which joins them.

It was here that Maxwell missed an important opportunity. He had thus ignored one of his own proposed laws for which Q was simply -l/r and which gave him the equally-simple force components:

What Maxwell failed to recognize was that the most general law of electrodynamics is not one which applies to two electric charges in isolation. If there were only two interacting electric charges in the whole universe they would have to move about one another in elliptical (or circular) motion or would be moving towards or away from one another in a common line. They would always be moving parallel or anti-parallel. In such a situation Maxwell’s law in (18) would satisfy the same condition as Ampere’s law, that the forces between the charges would be equal and opposite and directed along the line joining them. However, it would be better than Ampere’s law, because the force would have the simple inverse square of distance form. The magnitude of the force would be independent of the direction of r in relation to that of the charge velocities. It would be a law resembling Newton’s Law of Gravitation in that there would be mutual attraction between like current elements.

Furthermore, since in the general case the interaction force of two charges is merely a component of multiple interactions due to the presence of numerous other charges in motion, we need not be bound to the balance of action and reaction for each such component. There can be complete conformity with Newton’s Third Law of Motion for the aggregate effect of a system of charge satisfying any of the possible formulations of the component law. Of course, the component law must, as just indicated, remain the same and be valid in the ultimate situation of two isolated charges moving under their mutual interaction.

Maxwell had himself formulated the law. He failed to see its significance and opted for the Ampere version. He had introduced his third law of electrodynamics with the words:

We might, if we pleased, assume that the attraction between two elements at a given distance is proportional to the cosine of the angle between them. In this case Q =-l/r.

Note then that this assumption by Maxwell is exactly the form we have deduced for the force F, as given by (9). The force is simply (v.V)/c² times the Coulomb interaction force. Here, we have introduced the speed of light parameter c to convert the electro magnetic units of charge into electrostatic units.

Maxwell’s third law of electrodynamics must therefore be the correct empirical law for interaction between the charge carriers in normal electric circuits, that is for interactions between electrons. In vector notation it has the form:

When integrated over a closed path to express the action of an element i’ds‘ on the complete circuit s carrying current i, the middle term in (19) vanishes. The remaining terms then combine to become:

which is the Lorentz law of force.

The expression (19) is, as expected, of the form we found in (14) when the latter applies to actions between electrons. We find, therefor, that even from the classic work of Maxwell the law of electrodynamics is supported experimentally.

 

However, we must remember that the law of electrodynamics applies between two charges in motion and, in general, there will be numerous charges involved in electrodynamic interactions. The law applies to all combinations of charge pairs in the system and they all share the same electromagnetic reference frame. The velocities of the interacting charges are measured relative to this frame. It is a nonrotating frame, consistent with the inability of the electrodynamic interaction to generate a turning action and exchange angular momentum with the interacting charges. On the other hand, as we see from Fig. 5, the individual charge interactions can, owing to the electrodynamic action, develop an out-of-balance linear force, seemingly asserted by the electromagnetic frame itself. Such noncompliance with Newton’s Third Law of Motion is also apparent from the Biot-Savart or Lorentz law. This is a well discussed theme in the literature on electrodynamics and it does not mean that there will be any net out-of-balance force when such forces are summed for a whole system of charge.

Indeed, Newton’s Third Law of Motion is strictly valid only when applied to a complete system. When currents flow in interacting closed, and therefore complete, circuits, the mutual forces comply fully with this law of action and reaction balance. Even in the incomplete system, such as the general arrangement of two moving charges shown in Fig. 5, there may be more than the mere interacting charge present. Some authors complete the system by including radiation and its changing momentum is deemed to provide the force balance. But it may well suffice to recognize that the electromagnetic frame can be part of the whole system and mayitself be able to assert force transiently to cater for the sporadic unbalance of force as two charges coexist in the general configuration of Fig. 5.

In developing (I5) from (14) it was found that when two charges of identical mass move parallel there is strict balance of force and direct inverse-square law action between the charges. However, when the action is between charges of different mass, even parallel motion gives scope for out-of-balance force. One may then wonder what empirical evidence may exist in support of such dependence of the law of electrodynamics upon the mass ratio of the interacting charges.

The author has drawn attention to the early evidence of this from experiments on the anomalous cathode reaction forces associated with the vacuum arc (Aspden, 1969)[5].* More recently there has been mounting evidence, as we shall see in discussion at the end of this work, that there are anomalous acceleration forces acting on ions in plasma. Suffice it here to mention that Sethian, Hammer and Wharton (1978)[6]* have found:

experimental evidence for an anomalous electron-ion energy transfer in a relativistic-electron-beam-heated plasma that is 10³ times faster than can be predicted by classical processes.

At the end of the paper, the authors suggest ‘without particular justification’ that the anomalous factor might be the hydrogen ion to electron mass ratio, as applied in evaluating classical energy relaxation times in hydrogen. Thus the mass ratio M/m as used in the general law of electrodynamics (14) is in evidence as an anomalous acceleration of an ion by the action of electrons.

Clearly, such research, which is of great importance in fusion research where the object is to contain energy in the ions, can benefit from a solution of the unified field problem.

In proceeding, note that the word ‘relativistic’, as used in the above quotation, is intended to convey nothing other than that the electrons move at a high speed that is a significant fraction of the speed of light. There is no suggestion in the paper that the Theory of Relativity has any answers to offer in explaining the anomalies regularly reported in the electron-ion interaction.

It is of interest to examine what relativity does have to say on the subject of the electrodynamic law. Note that we arrived at the Lorentz Law of Force in (20). It applies to interaction involving a complete circuit, but it has been taken to apply as the corresponding BiotSavart formulation to interaction between isolated pairs of charge in motion.

It was not until 1903 that an experiment was performed by Trouton and Noblet involving two parallel-moving charges, neither forming part of a closed circuit, but isolated on the plates of a charged capacitor[7]. The mutual force was found to be directed along the line joining the charges and asserts no turning couple on the capacitor, as expected from (20). The motion was attributed to that of the Earth through space. The experiment is, therefore, not conclusive if one presumes that the Earth’s electromagnetic reference frame moves along with it in its motion through space. It is inconclusive inasmuch as an observer moving with the Earth will, by the relativistic argument, not sense any motion of charge on a capacitor moving with the observer. However, at the time of the experiment it could have been said to disprove the general application of the Lorentz law to charges in isolation. It did support the third law of electrodynamics presented by Maxwell, but appears not to have been considered in this context. Indeed, so far as the author is aware, the extra empirical fact provided by the Treuton-Noble experiment and needed to derive the empirical law of electrodynamics was not used for this purpose until the author examined its relevance (Aspden, 1969).[8]*

Lorentz lost no time in reacting to the Trouton-Noble experiment because in 1904 he defended his law against the Trouton-Noble result by presenting his transformations and the contraction hypothesis.

The fact that the Lorentz law can be derived from Einstein’s later theory is also no confirmation that it must be valid for action between isolated charge. The derivation in both cases depends upon the use of certain transformations with Maxwell’s field equation:

Here V is the electric field intensity and H is the magnetic field intensity. t is time.

 

The equation was based upon an experimental observation involving the electromotive force in a closed wire loop. It was asserted that it applied equal1y to the total E.M.F. round any closed curve. As we then read from the text ‘The Classical Theory of Electricity and Magnetism’ by Abraham and Becker (1932):

 

However, this … is in its complete generality a hypothesis, which

we must justify by testing its consequences.

Its consequences have only been verified for actions involving closed circuits. The transformations in relativity implicitly introduced closed circuit conditions. Hence the Lorentz law of force cannot be relied upon in spite of its derivation from relativistic principles.

Inverse-Square Laws of Force

Much of accepted field theory is based upon the experimental foundation of Coulomb’s Law and the observed propagation of electromagnetic waves. Maxwell’s equations provide a well-tested starting point in field theory and are all the more secure because they have a linear form and are not affected by relativistic transformation. The fields represented can be superimposed and added vectorially. However, had the equations contained second-order terms, signifying energy density parameters, then the impact of relativity may well have been a different story.

In contrast, Coulomb’s Law and Newton’s Law of Gravitation both depend upon interactions which are second-order in this sense and both present difficulties when extended to relate to dynamic interactions.

Following the empirical example used in connection with the law

of electrodynamics, we will study the interaction of bodies subject to an inverse-square of distance law of mutual force, but without adopting any field hypothesis. OUf sole consideration will be the energy we associate with the interaction, taking energy as a scalar quantity and so avoiding the complications of the vector field.

 

The task is to derive a general formula j(x, r) for the distribution denoting the element of energy  a distant x from a body A and contained within a spherical shell of thickness  centered on that body. E is the energy associated with the interaction between body A and body B distant r from A. We know, since we are dealing with an inverse-square law of force, that the mutual force of attraction F is given by:

F=k/r²                       (22)

K is a constant which can be positive or negative for the Coulomb interaction, but which is invariably positive for the Newtonian gravitational interaction.

 

The force F can be expressed as a partial derivative of the energy E governing the interaction, with respect to the separation distance r,

thus:

This also assures that action balances reaction, there being a mutual force of strength F asserted on A and B. Introducing x, this becomes:

Our problem then is to determine the general solution forf(x, r)which brings (24) into accord with (22).

The function/(x, r) can be regarded as a function of x or r together with terms in xlr or terms in rlx. Then, bearing in mind that the energy under consideration is finite, given a finite value of r, we can expect/ex, r) to be represented by a convergent power series in (xlr) when x is smaller than r or a convergent power series in(rlx) when x is larger than r. This follows from Maclaurin’s Theorem. It may then be shown that the general solution must have the form:

where the summation applies to all integral values of n. The coefficients Cn need to be determined, but to assure convergence they will be zero for n positive whenx is large and for n negative when x is small.

With n=0 or n= -I we must have Cn = 0, because the integral in (24) would be otherwise be infinite.

Next, we observe that the function/(x,r) can be restricted by the condition that it is invariable with r beyond a certain distance commensurate with r. This asserts that whatever the cause of the force interaction it is local to the immediate environment of the two interacting bodies. We are supposing that the energy E is located in the near vicinity of the bodies and that should some of this energy be remote its effect will be of little consequence to the interaction. In making this assertion one must depart from the idea embodied in the Mach Principle that remote stellar matter determines gravitational interaction locally. Our hypothesis is that force is connected solely with the interaction energy local to the two interacting bodies and we are guided to this hypothesis by the fact that the forces are not unduly retarded, as they would be if the energy had to migrate to and from remote areas.

Formulating this condition:

for all x, when x is appreciably greater than r. Restricting ourselves to this latter range, we combine (25) and (26) to obtain:

Evidently n is -2 and all other Cn values applicable for the range where x is large must be zero.

This result is consistent with the argument that the applicable law of force must be dependent upon processes which somehow correlate with the symmetry of space. For example, a symmetrical emission from a point source has an intensity which diminishes as the square of distance from the source. Such an action suggests that only one term in n would apply in a general formulation such as (25), at least over the same range of x, as it seems unlikely that a multiplicity of physical actions could be involved in the same region of space, each action having a different symmetry connection and corresponding to a different term inn. Probably, therefore, the expression f(x, r)will contain but a single (x/r)n term over a given range of x, as we have just found where x is large in relation to r.

Since we are considering the distribution of energy in space it is helpful at this stage to examine two possibilities. Firstly, case (a) for which the interaction energy tends to be as close as possible to either body as reference and, secondly, case (b) for which the interaction energy tends to be as remote as possible from either body as reference. This is of interest because there are two basic inverse-square laws, Newton’s Law of Gravitation and Coulomb’s Law and there is a physical difference which poses questions. With gravitation like bodies mutually attract and with the electrostatic interaction like bodies mutually repel The energy transfer processes could then be different in the two cases, one finding its energy from a primary source which tends to minimize and so forces a higher concentration of local energy in the reaction process and the other being, in fact, a process involving the primary energy which seeks to feed a reaction and so diminishes locally.

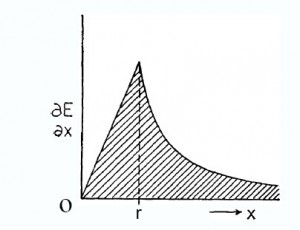
The solution for the case (a) interaction has a unique form if we specify that it must be the most simple solution having a single transition in the form of(xlr)n at the distance x=r determined by the physical spacing of the two bodies. For x greater than r we have found that n =-2. For x less than r the tendency of E to be as close to the reference body A as possible means that n must be as low as possible. We also know that the convergence requirement means that n is a positive integer over this range. Hence n=I. The resulting spatial energy distribution for case (a) is shown in Fig. 12, drawn to avoid an energy discontinuity at x=r.

As will be shown, there are reasons for identifying this particular energy distribution with the gravitational interaction.

 

 

The solution for case (b) requires the interaction energy to be as remote from the reference body as possible. This is the case for the unique solution that there is no energy at all over the range of x from

O to r. The interaction energy is all confined to the space beyond x=r, where the (xlr)-2 term applies. The resulting energy distribution is shown in Fig. 13.

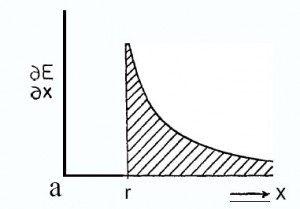
Note that we are considering energy summed within concentric shells of space centered on either A or B as reference body and not interaction energydensities. These do have finite positive or negative values within the range from x=0 to x=r.

The particular energy distribution of Fig. 13 may be readily identified with Coulomb interaction by analysis based upon classical field theory. This will be our starting point in the next chapter. Also, our objective will be to progress in the quest to unify the gravitational and electromagnetic force by examining the spatial energy distribution of the electrodynamic interaction in relation to Fig. 12.

 

---